19.4 AR(1)
A stationary stochastic process \((Y_t)\) follows an AR(1) model if
\[Y_t=\delta +\phi_1 Y_{t-1}+\omega_t, \quad \forall t=\pm1, \pm2, \pm3, \ldots\]
where \((\omega_t)\) is a white noise the zero mean and variance \(\sigma^2_\omega, \,\, \rightarrow \,\, \omega_t \sim N(0,\sigma^2_\omega).\)
If the process is stationary in mean and variance then it is satisfied that \(E(Y_t) = E(Y_{t-1})\) and $Var (Y_t) = Var(Y_{t-1}), \(forall t\) so that:
\[ E(Y_t) = E(Y_{t-1})=\mu=\delta +\phi_1\mu \rightarrow \mu=\frac{\delta}{1-\phi_1} \] \[ \gamma_0 = Var(Y_t) = Var(Y_{t-1})= \phi_1^2\gamma_0 +\sigma_\omega^2 \rightarrow \gamma_0 = \frac{\sigma_\omega^2}{1-\phi_1^2} \]
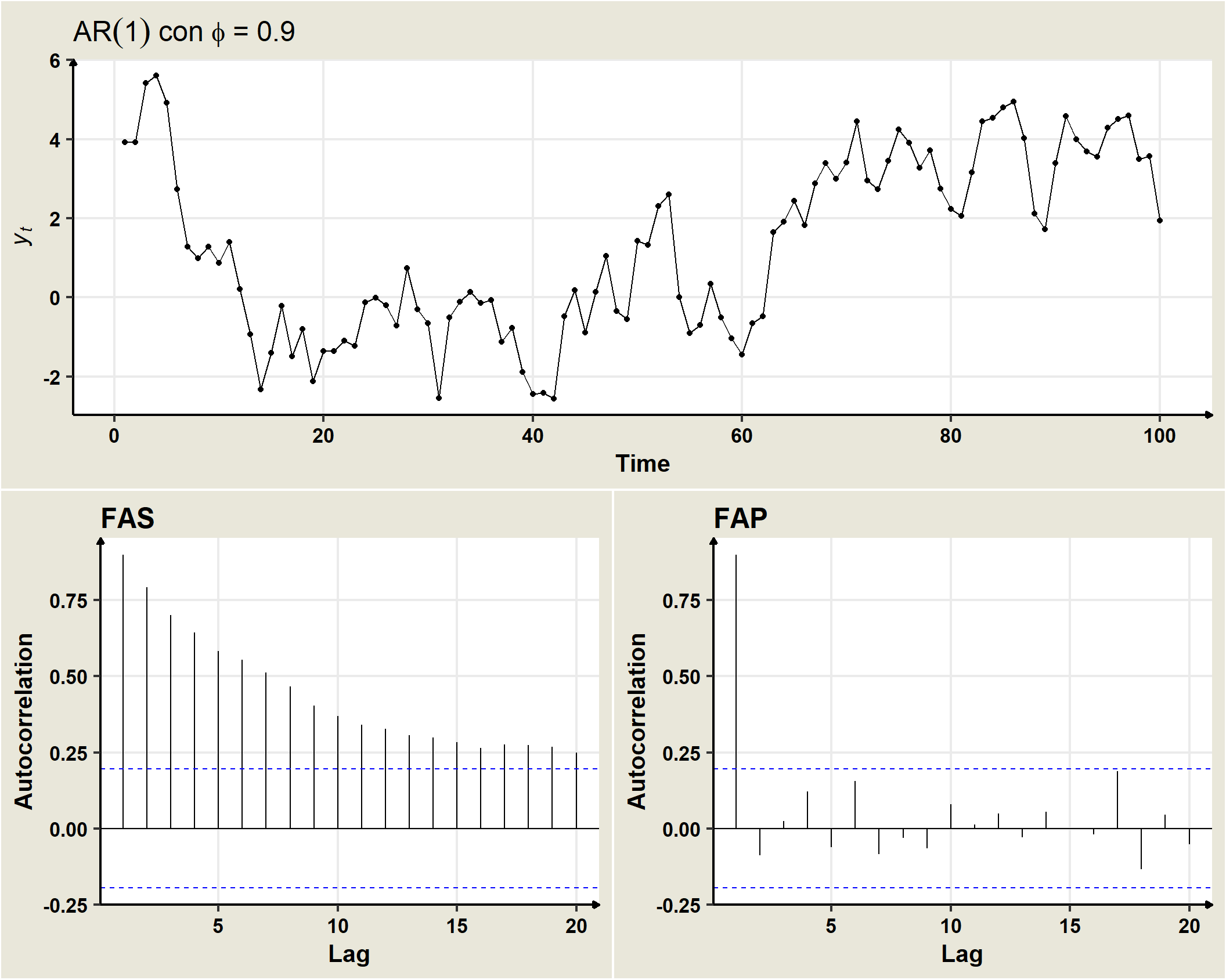
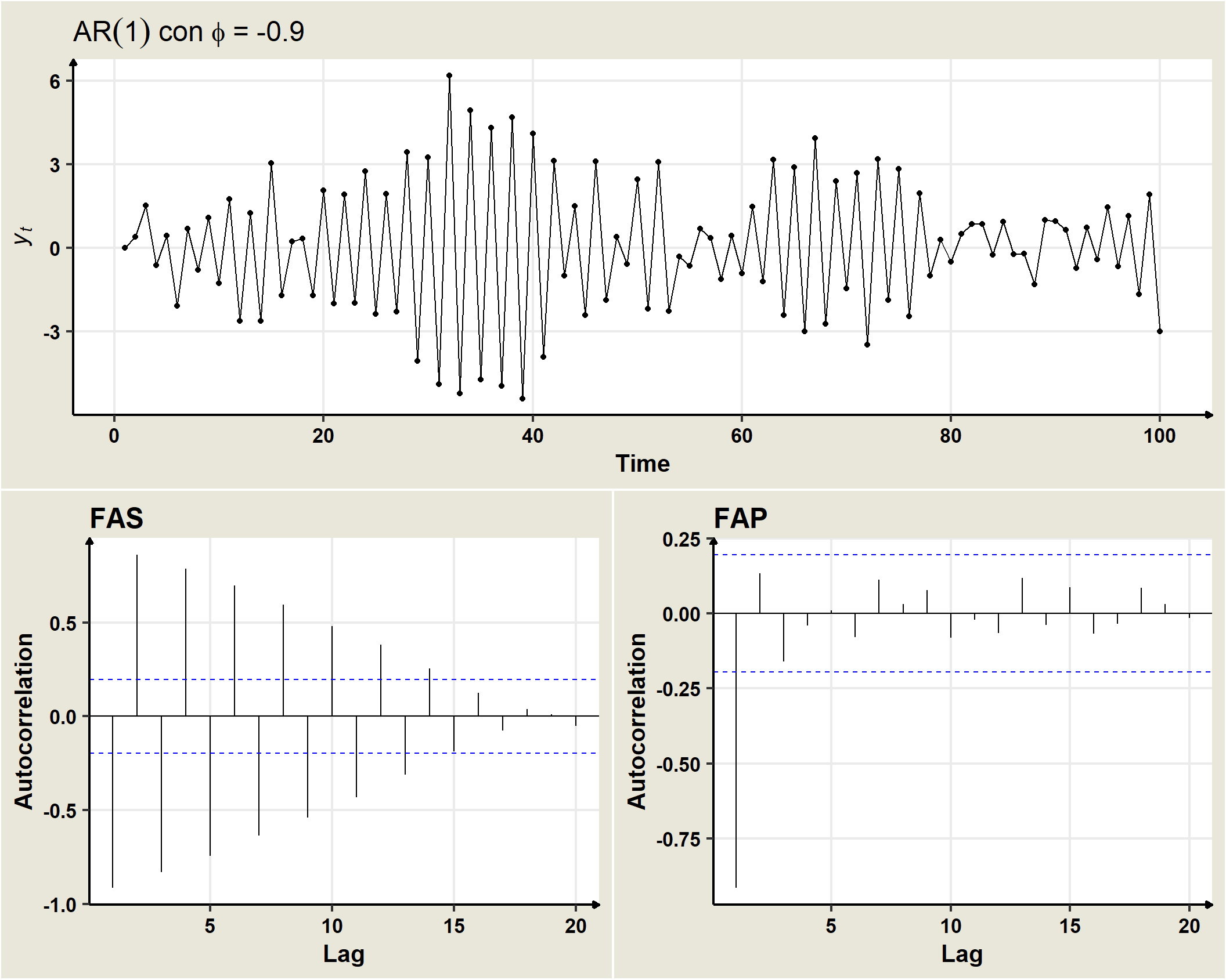
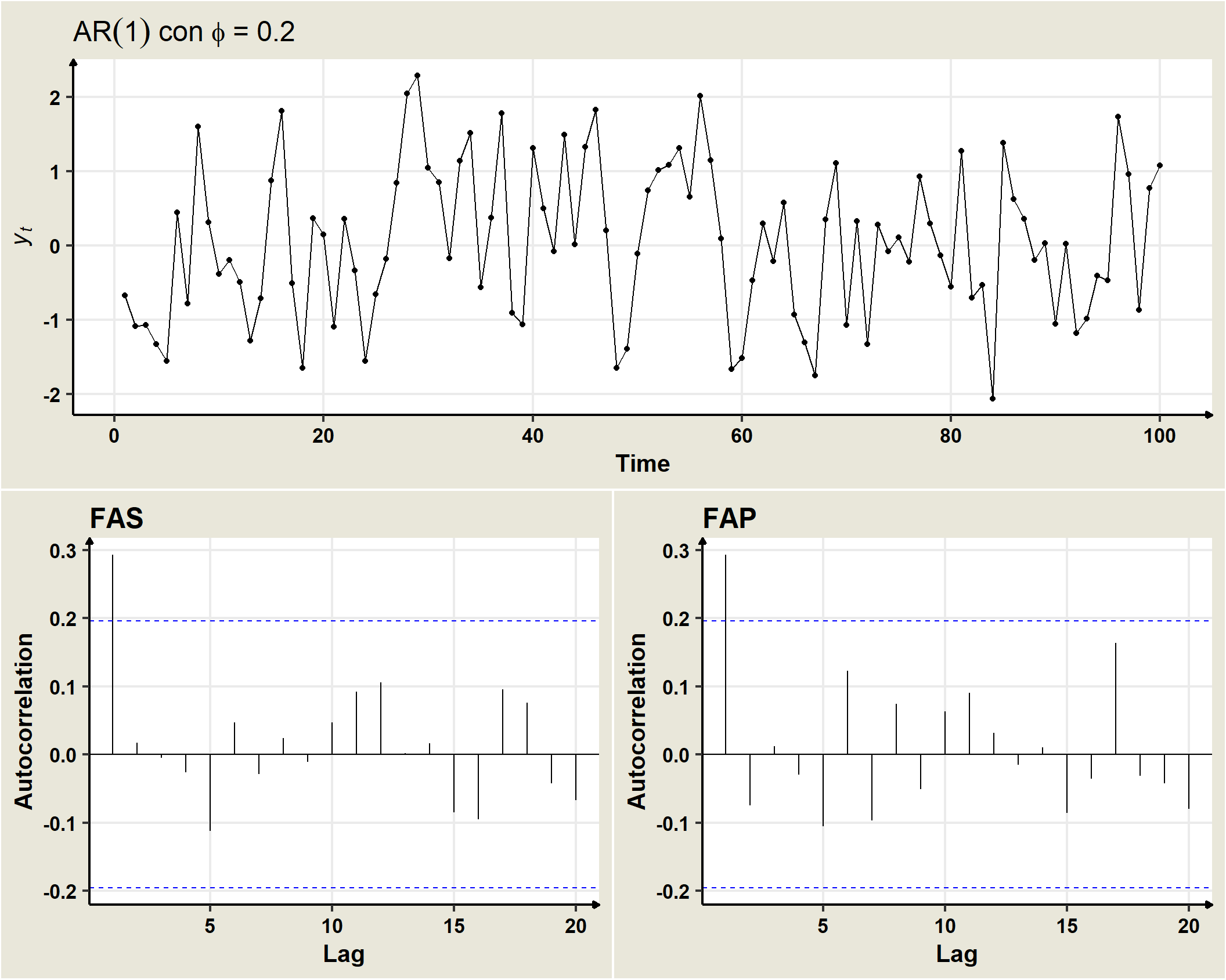
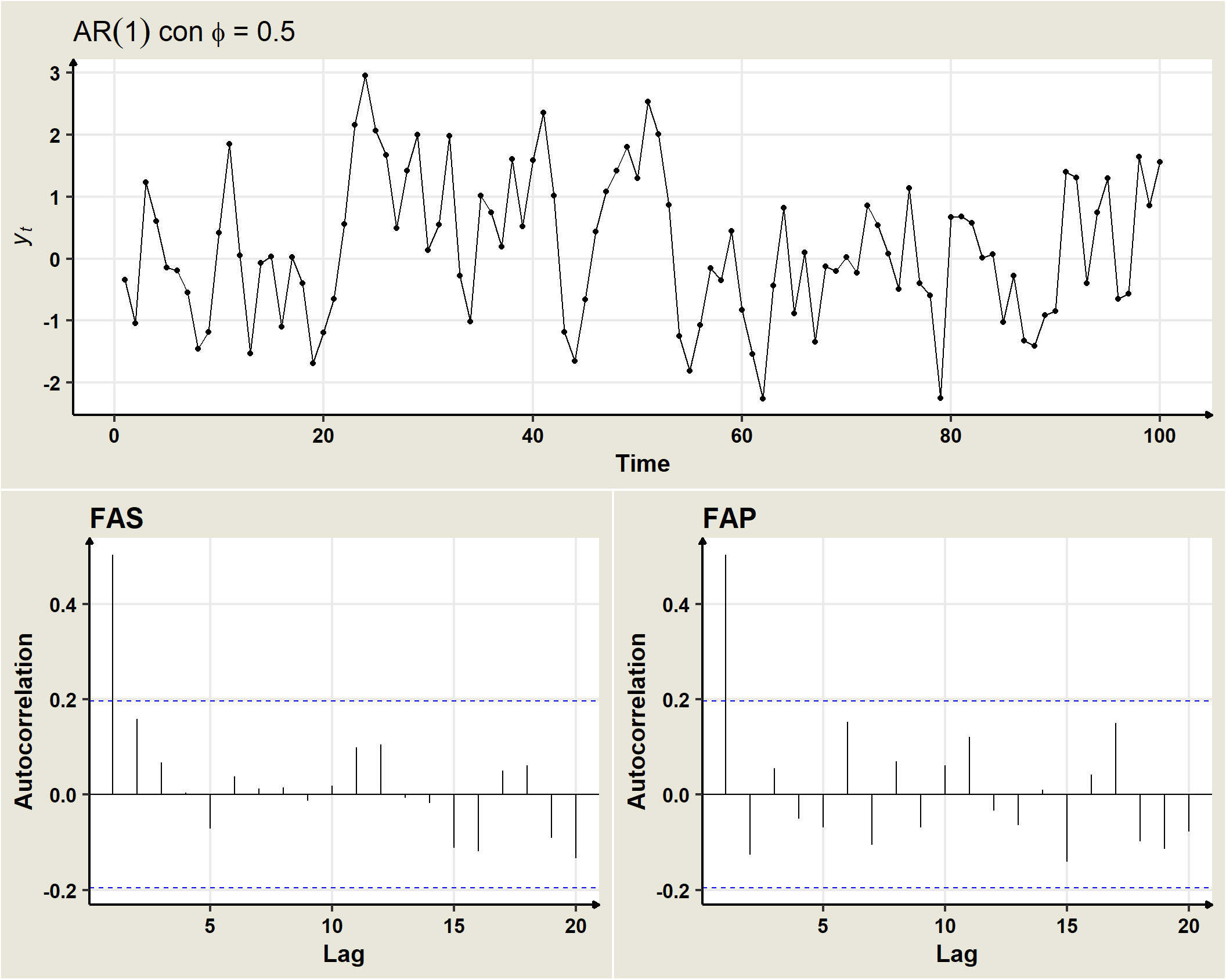
The condition to be fulfilled for \(\mu\) and \(\gamma_0\) to be positive and finite is that $ | _1 | <1$ (invertibility condition). In that case, the process will be stationary in mean and variance. Similarly, if the process is stationary, it will also be verified for the covariances that:
\[ \begin{aligned} \gamma_k & = E[Y_t Y_{t-k}] - E[Y_t]E[Y_{t-k}]\\ & = E[(\phi_1Y_{t-1} + \omega_t) Y_{t-k}]\\ & = \phi_1E[Y_{t-1}Y_{t-k}] + E[\omega_t Y_{t-k}]\\ & = \phi_1 \gamma_{k-1} =\phi_1^2 \gamma_{k-2} = \phi_1^3 \gamma_{k-3} =\ldots = \phi_1^k \gamma_{0}\\ & \rightarrow \rho_k = \dfrac{\gamma_k}{\gamma_0}=\dfrac{\phi_1^k\gamma_0}{\gamma_0}=\phi_1^k \end{aligned} \]
where, without loss of generality it has been assumed that \(E[Y_t]=\mu=0\)