19.2 Random walk
A non stationary stochastic process \((Y_t)\) is a random walk when:
\[Y_t=Y_{t-1} + \omega_t\]
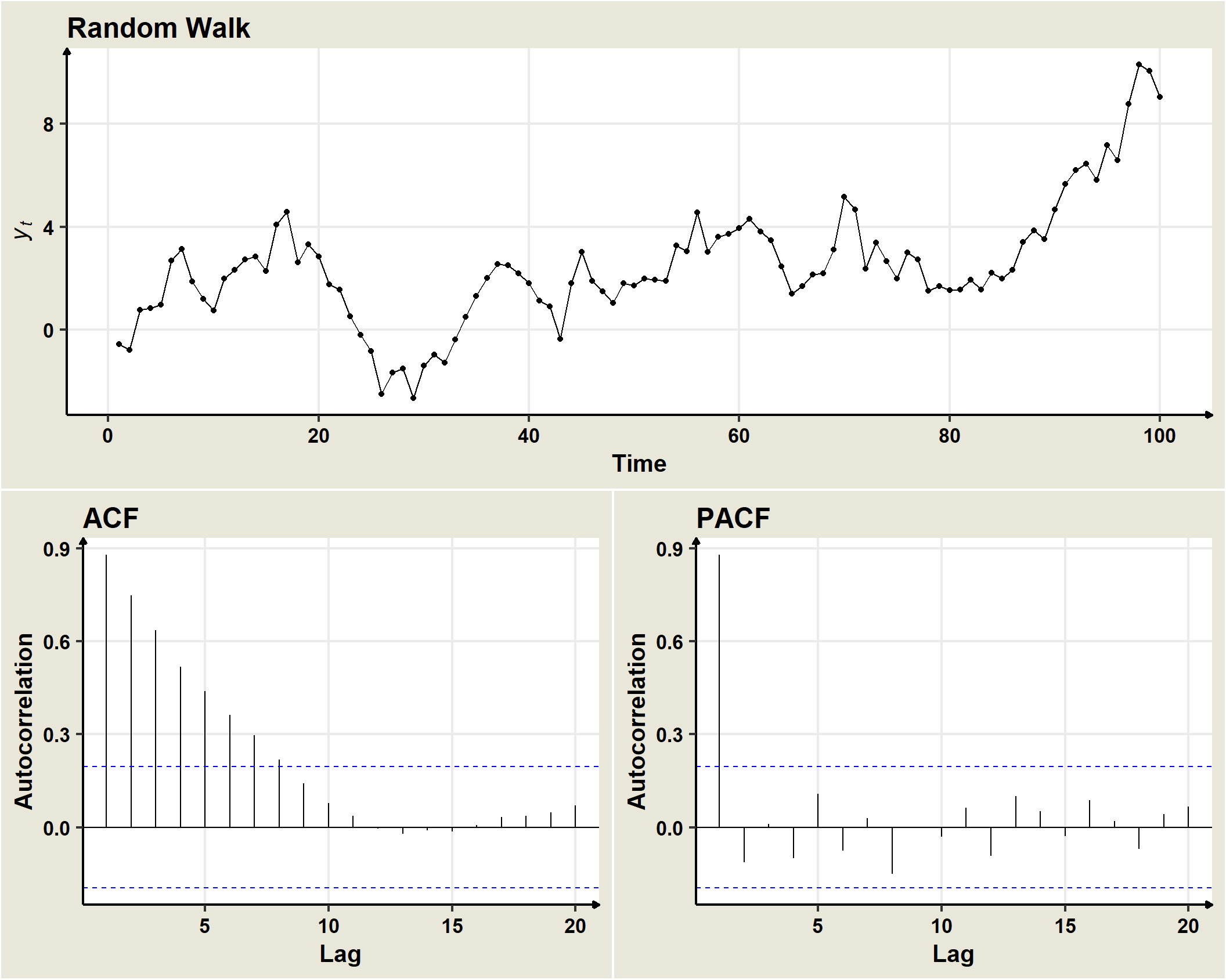
- A random walk is a stochastic process whose first difference is a white noise, i.e.
\[Y_t - Y_{t-1}=\omega_t\] * Sometimes an additional parameter is included:
\[Y_t = \mu + Y_{t-1} + \omega_t\]
- A random walk can be written as:
\[\nabla Y_t = \mu + \omega_t,\]
so that a non-stationary stochastic process \((Y_t)\) is a random walk when its regular difference of order 1 \(\left(Y_{t} \right ) \equiv \left ( Y_{t}-Y_{t-1} \right )\) is a stationary process.