19.1 Ruido Blanco

White Noise is a stochastic process in which the component random variables are uncorrelated with each other, have mathematical expectation equal to zero and constant variance equal to $\sigma^2$.

Gaussian white noises are formed by a succession of random variables with Normal distribution, zero expectation, constant variance and serially uncorrelated with each other. That is, if

$\omega_t \sim N(0,\sigma^2)$ is a Gaussian white noise, then $cov(\omega_t,\omega_{t+k})=0$

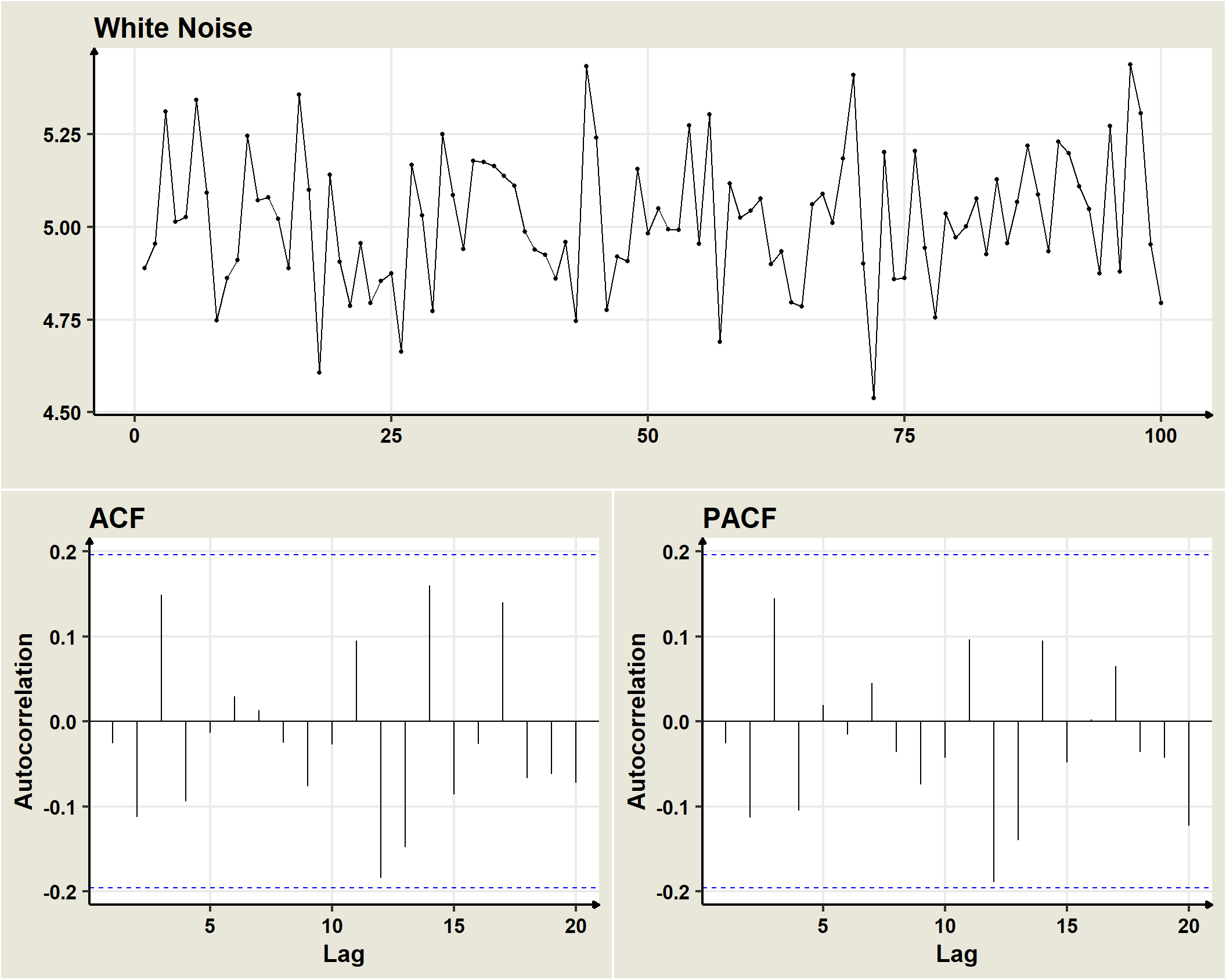
In general, a univariate white noise process is a sequence $(\omega_t)$ of identically and independently distributed random variables with mean $0$ and variance $\sigma^2_omega$, which is represented as

\[\omega_t \sim IID(0,\sigma^2_\omega)\]

Each $\omega_t$ follow a Normal distribution, $(\omega_t)$ is a Normal or Gaussian White Noise Process.

We assume that the errors of the processes we will see next are Gaussian white noise, formed by a succession of random variables with Normal distribution, zero expectation, constant variance and serially uncorrelated with each other.
That is, if $(\omega_t)$ is Gaussian white noise, then $\omega_t \sim N(0,\sigma^2_\omega)$ and $cov(t,{t+k})=0.