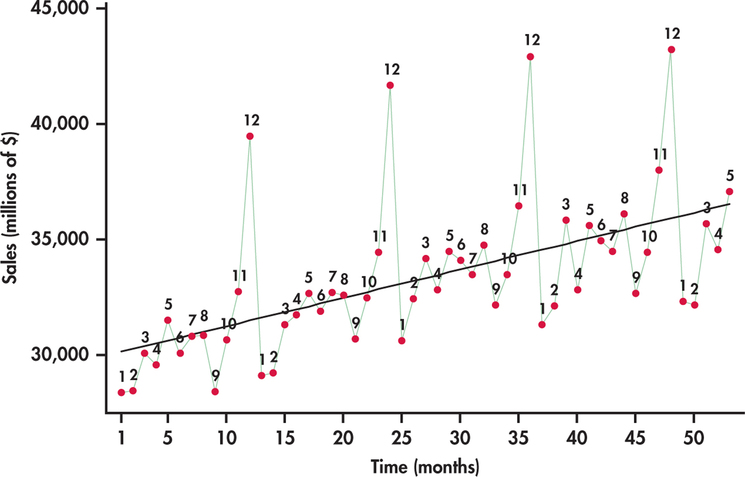
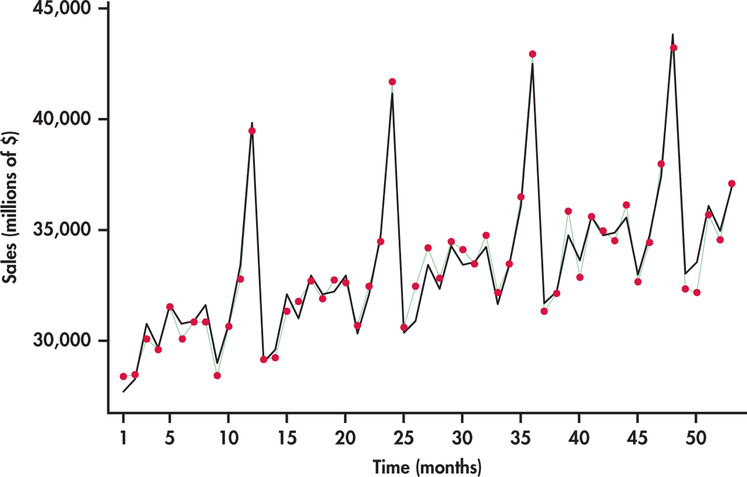
15.3 Modeling Seasonality

• By definition, Seasonality is a change in the mean of the series that repeats periodically every \(s\) seasons. If the series is monthly, \(s=12\); if quarterly, \(s=4\); if weekly, \(s=52\) or \(53\), etc.

• A deterministic way of capturing seasonality consists of defining dummies variables (with values 0 or 1). For example, for a monthly series define the twelve dummies corresponding to: January (\(S1\)), February (\(S2\)), \(\ldots\), December (\(S{12}\)) and fit the regression model:

\[ s_{t}=\beta_{1} \mathrm{~S} 1_{t}+\beta_{2} \mathrm{~S} 2_{t}+\ldots+\beta_{12} \mathrm{~S} 12_{t} \] As observed, this model does not have an intercept. If the model includes an intercept, only 11 dummies are used.