15.2 Modeling the trend
The simplest models for trend are regressions of the variable \(y\) with respect to time..
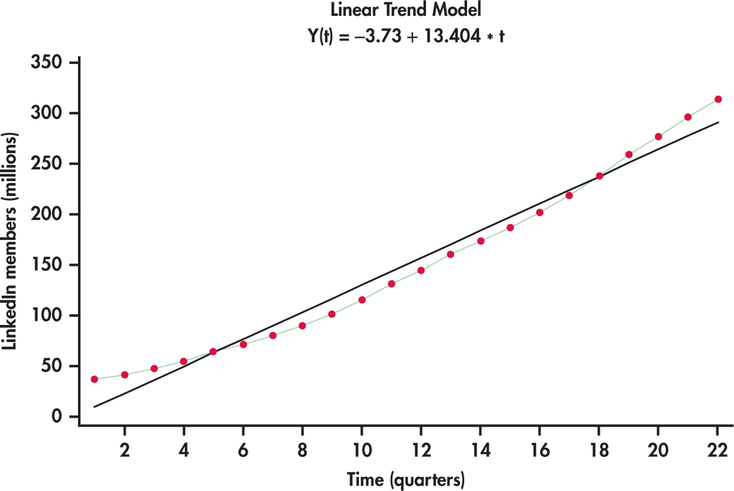
A linear trend model is:
\[t_{t}=\alpha_{0}+\alpha_{1} t, \,\, \,\, \forall t=1,2, \ldots, T.\]
The parameter \(\alpha_{1}\) represents the slope and describes the expected growth between two periods. The forecast of the variable \(y\) for the period \(T+k\) is:
\[\hat{y}_{T}(k)=\hat{\alpha}_{0}+\hat{\alpha}_{1}(T+k)\]
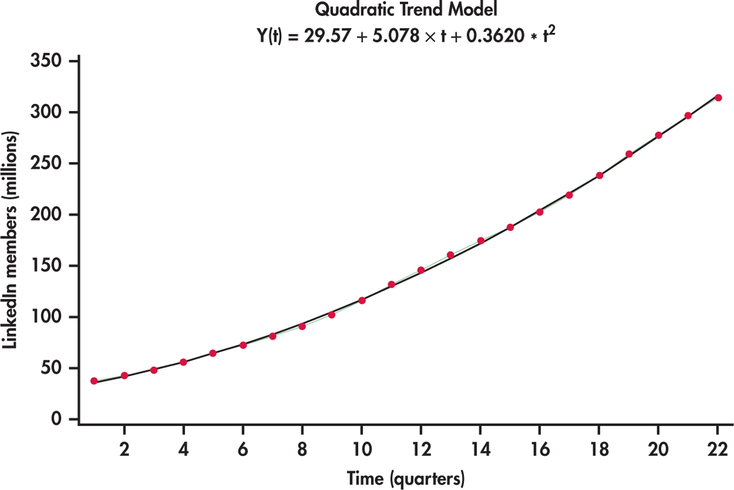
- A quadratic trend model is:
\[t_{t}=\alpha_{0}+\alpha_{1} t+\alpha_{2} t^{2}, \,\,\,\, \forall t=1,2, \ldots, T.\]
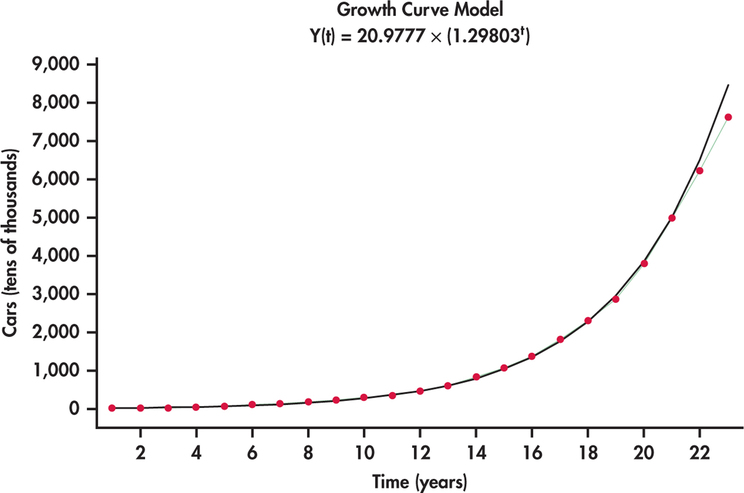
- An exponential trend model is:
\[ t_t = \exp \left ( \alpha_0 +\alpha_1 t \right ) .\]
By taking logarithms is:
\[\log t_{t} = \alpha_{0} + \alpha_{1} t + \varepsilon_{t}\]