9.1 Confusion Matrix

The confusion matrix shows the number of correct and incorrect predictions made by the model compared to the actual results in the data. The confusion matrix is a matrix \(n\)times n$, where \(n\) is the number of classes.

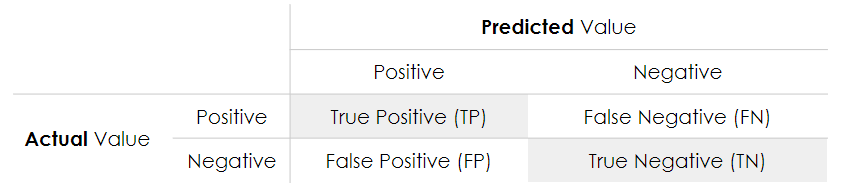
In our example:

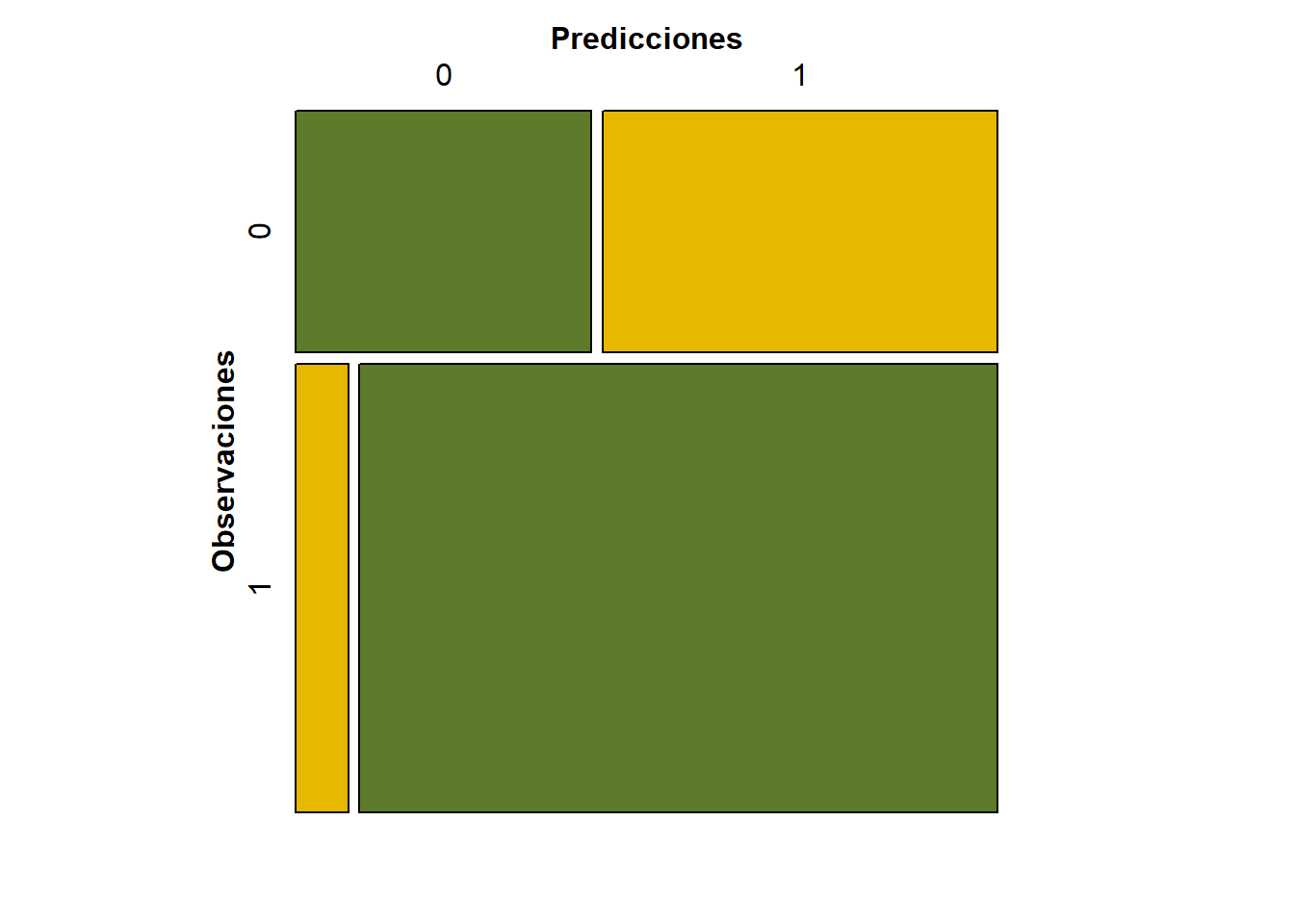
• Accuracy: the proportion of the total number of correct predictions.

\[ACC = \frac{TP+TN}{TP+TN+FP+FN}\]

• Positive Predictive Value: the proportion of positive cases that were correctly identified.

\[PPV = \frac{TP}{TP+FP}\]

• Negative Predictive Value: the proportion of negative cases that were correctly identified.

\[ NPV = \frac{TN}{TN+FN} \]

• Sensitivity or Recall: lhe proportion of actual positive cases that are correctly identified.

\[TPR = \frac{TP}{TP+FN}\]

• Specificity: the proportion of real negative cases that are correctly identified.

\[TNR = \frac{TN}{TN+FP}\]

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction No Yes
##        No  15  20
##        Yes  5  60
##                                           
##                Accuracy : 0.75            
##                  95% CI : (0.6534, 0.8312)
##     No Information Rate : 0.8             
##     P-Value [Acc > NIR] : 0.91252         
##                                           
##                   Kappa : 0.3902          
##                                           
##  Mcnemar's Test P-Value : 0.00511         
##                                           
##             Sensitivity : 0.7500          
##             Specificity : 0.7500          
##          Pos Pred Value : 0.9231          
##          Neg Pred Value : 0.4286          
##              Prevalence : 0.8000          
##          Detection Rate : 0.6000          
##    Detection Prevalence : 0.6500          
##       Balanced Accuracy : 0.7500          
##                                           
##        'Positive' Class : Yes             
##