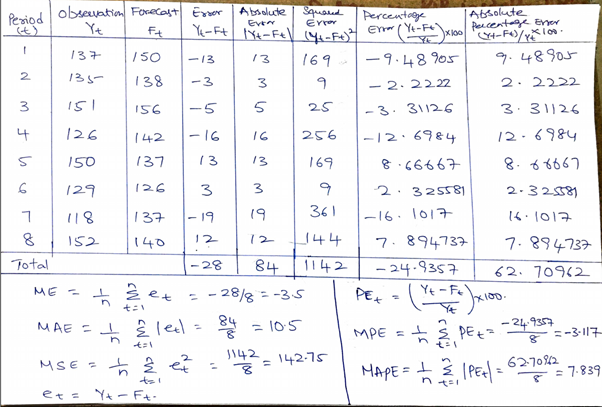
23 Forecast Error

If, generically, for the period \(t\) a prediction is made with the information available at \(t-1\), which we denote by $ $\(hat{y}_{t|t-1}\), for the period \(t\) we can make a comparison of this value with the one we actually observe (\(y_t\)). The difference between both values will be the prediction error one period forward and will be given by:

\[ e_{t | t-1}=y_t-\hat y_{t| t-1} \]

To quantify the overall prediction errors, the following statistics are used: the Root Mean Squared Error (RQE) and the Mean Absolute Error (MAE).

In the case that \(T\) observations are available and forecasts have been made from the observation \(2\), RECM and EAM are given by

\[ RECM=\sqrt{\frac{\sum_{t=2}^T (y_t-\hat y_{t/t-1})^2}{T-1}} \]

\[ EAM=\dfrac{1}{T-1}\sum_{t=2}^T \left(y_t-\hat y_{t/t-1}\right)^2 \]

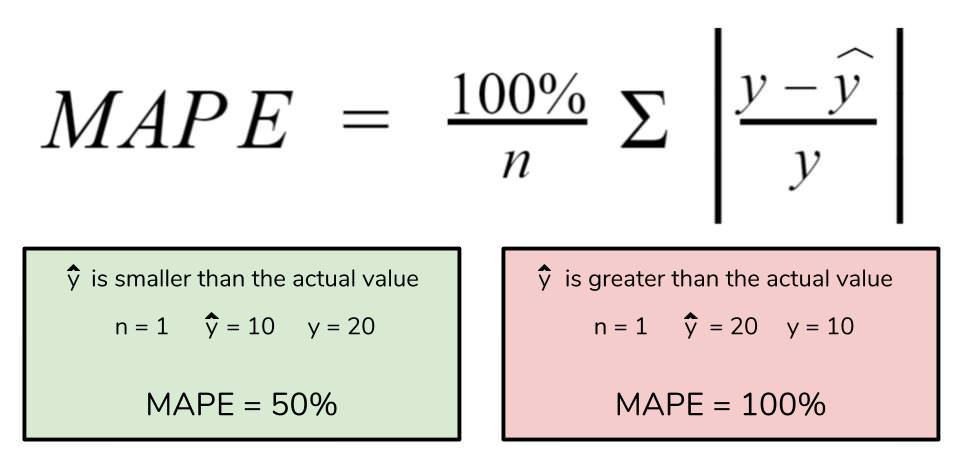
We can also use the MAPE, Mean Absolute Percentage Error.

\[ MAPE=\dfrac{1}{T-1}\sum_{t=2}^T \left( \dfrac{ \hat y_{t/t-1}}{y_t} \right) \]