5.3 Probabilities
A logistic regression model allows us to establish a relationship between a binary outcome variable and a group of predictor variables. It models the logit transformed probability as a linear relationship with the predictor variables. More formally, let \(Y\) be the binary outcome variable indicating failure/success with \(\{0,1\}\) and \(p\) be the probability of \(y\) to be \(1, p=P(Y=1)\). Let \(x_{1}, \cdots, x_{k}\) be a set of predictor variables. Then the logistic regression of \(Y\) on \(x_{1}, \cdots, x_{k}\) estimates parameter values for \(\beta_{0}, \beta_{1}, \cdots, \beta_{k}\) via maximum likelihood method of the following equation \[ \operatorname{logit}(\pi)=\log \left(\frac{\pi}{1-\pi}\right)=\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{k} x_{k} . \] Exponentiate and take the multiplicative inverse of both sides, \[ \frac{1-\pi}{\pi}=\frac{1}{\exp \left(\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{k} x_{k}\right)} . \] Partial out the fraction on the left-hand side of the equation and add one to both sides, \[ \frac{1}{\pi}=1+\frac{1}{\exp \left(\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{k} x_{k}\right)} . \] Change 1 to a common denominator, \[ \frac{1}{\pi}=\frac{\exp \left(\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{k} x_{k}\right)+1}{\exp \left(\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{k} x_{k}\right)} \] Finally, take the multiplicative inverse again to obtain the formula for the probability \(P(Y=1)\), \[ \pi=\frac{\exp \left(\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{k} x_{k}\right)}{1+\exp \left(\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{k} x_{k}\right)} . \]
-
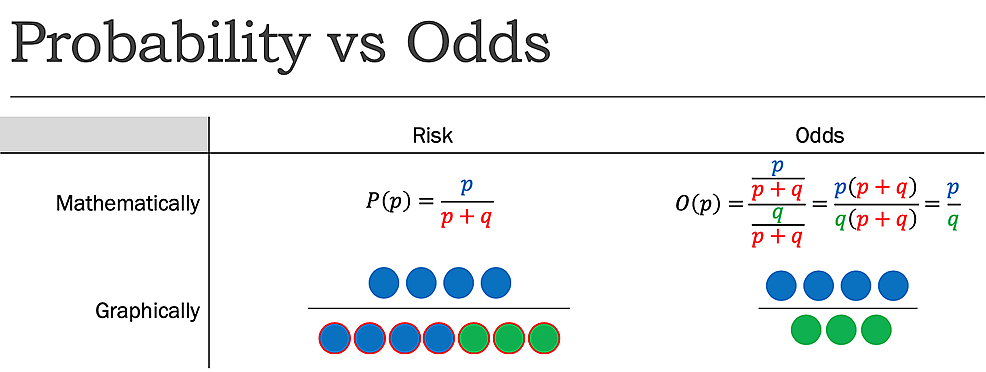
Probability: if the probability of success is \(\pi=0.8\), the probability of failure is \(1-\pi=0.2\)
-
Odds: It is the ratio between the probability of success and the probability of failure. \(\operatorname{odds}= \dfrac{\pi}{1-\pi}=\dfrac{0.8}{0.2}=4.\) That is, the odds of success are 4 to 1.
-
Odds Ratio: It is the ratio between Odds. \(\operatorname{OR}= \dfrac{\operatorname{odds}_1}{\operatorname{odds}_2}=\dfrac{\frac{\pi_1}{1-\pi_1}}{\frac{\pi_2}{1-\pi_2}}\)