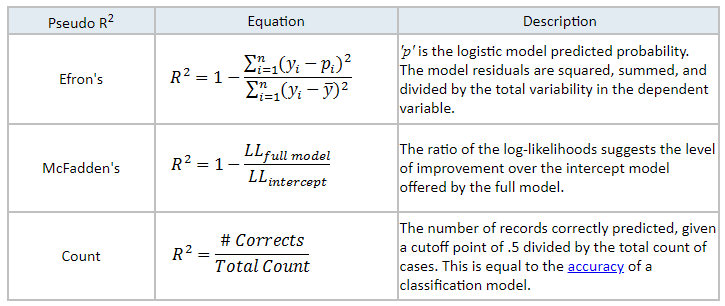
8.1 Pseudo \(R^2\)
Unlike linear regression models, logistic models do not use or have an equivalent to \(R^2\) that exactly determines the variance explained by the model.
Different methods have been developed known as $\(operatorname{pseudo}-R^2\) that attempt to approximate the concept of the coefficient of determination. They range from 0 to 1, but by no means can they be interpreted as the same as \(R^2\).
One of the \(\operatorname{pseudo}-R^2\) for logistic regression was proposed by McFadden’s:
\[ R^{2}_{\text{McFadden}} = 1- \frac{\log(L(M_1))}{\log(L(M_0))}, \]
where \(L\) is the value of the likelihood of each model. In this case, \(\log(L)\), has a meaning analogous to the sum of squares of linear regression. Hence it is called \(\operatorname{pseudo}-R^2\).
\(R^{2}_{\text{McFadden}}\) is equals to\(0\) if the fitted model does not improve on the null model, and a value of \(1\) if it fits the data perfectly.
- In our example:
\[\text{McFadden } R^2 = 0.142147,\]
Other pseudo-\(R2\):