19.1 Ruido Blanco
White Noise is a stochastic process in which the component random variables are uncorrelated with each other, have mathematical expectation equal to zero and constant variance equal to \(\sigma^2\).
Gaussian white noises are formed by a succession of random variables with Normal distribution, zero expectation, constant variance and serially uncorrelated with each other. That is, if
\(\omega_t \sim N(0,\sigma^2)\) is a Gaussian white noise, then \(cov(\omega_t,\omega_{t+k})=0\)
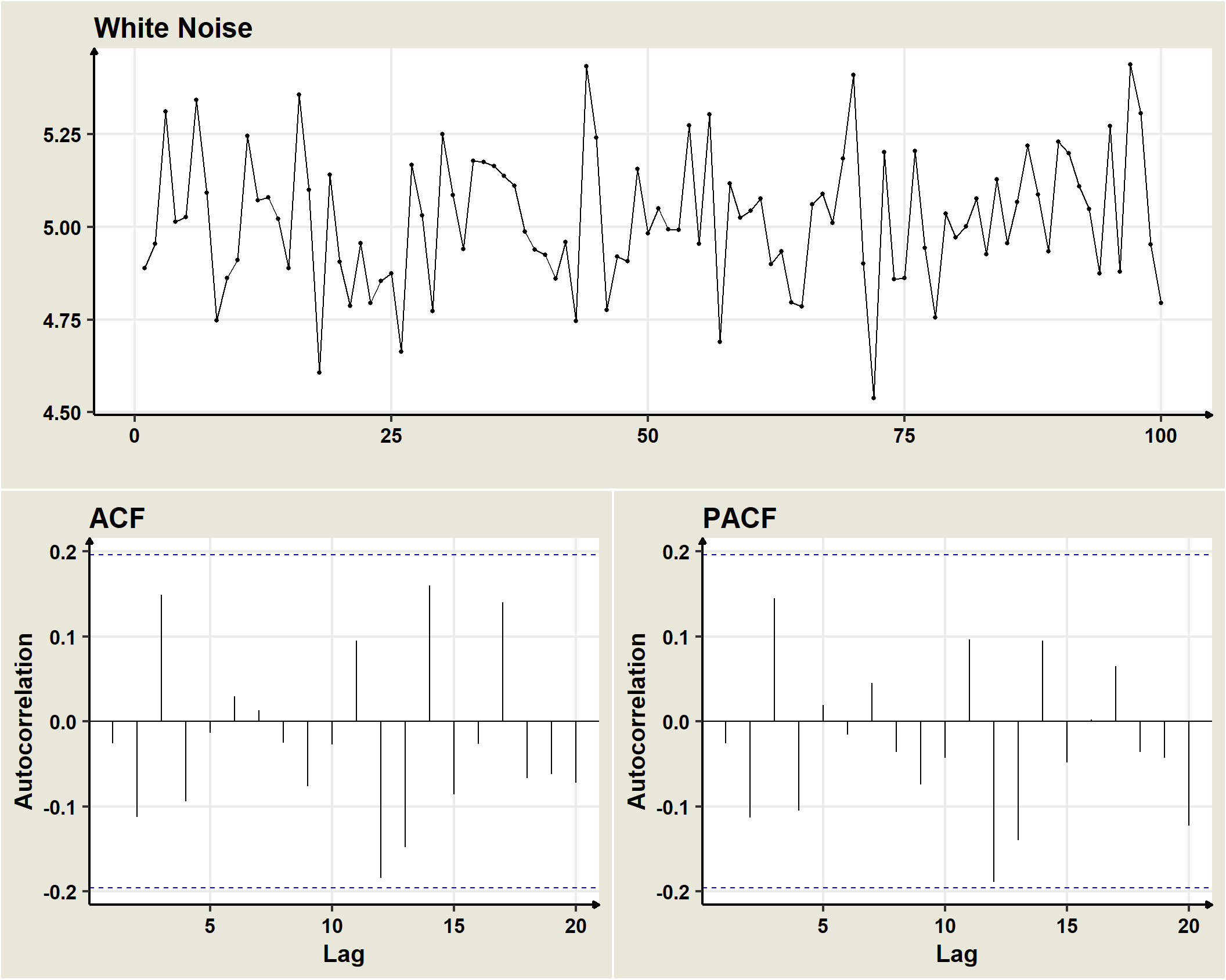
In general, a univariate white noise process is a sequence \((\omega_t)\) of identically and independently distributed random variables with mean \(0\) and variance \(\sigma^2_omega\), which is represented as
\[\omega_t \sim IID(0,\sigma^2_\omega)\]
Each \(\omega_t\) follow a Normal distribution, \((\omega_t)\) is a Normal or Gaussian White Noise Process.
We assume that the errors of the processes we will see next are Gaussian white noise, formed by a succession of random variables with Normal distribution, zero expectation, constant variance and serially uncorrelated with each other.
That is, if \((\omega_t)\) is Gaussian white noise, then \(\omega_t \sim N(0,\sigma^2_\omega)\) and $cov(t,{t+k})=0.