17.2 Stationarity

A stochastic process \(\left( Y_{t} \right)\) is stationary when the statistical properties of any finite sequence \(Y_{t_{1}}, Y_{t_{2}}, \ldots, Y_{t_{n}}(n \geq 1)\) of components of \(\left( Y_{t} \right)\) are similar to those of the sequence \(Y_{t_{1}+h}, Y_{t_{2}+h}, \ldots, Y_{t_{n}+h}\) for any integer $h= , , $.

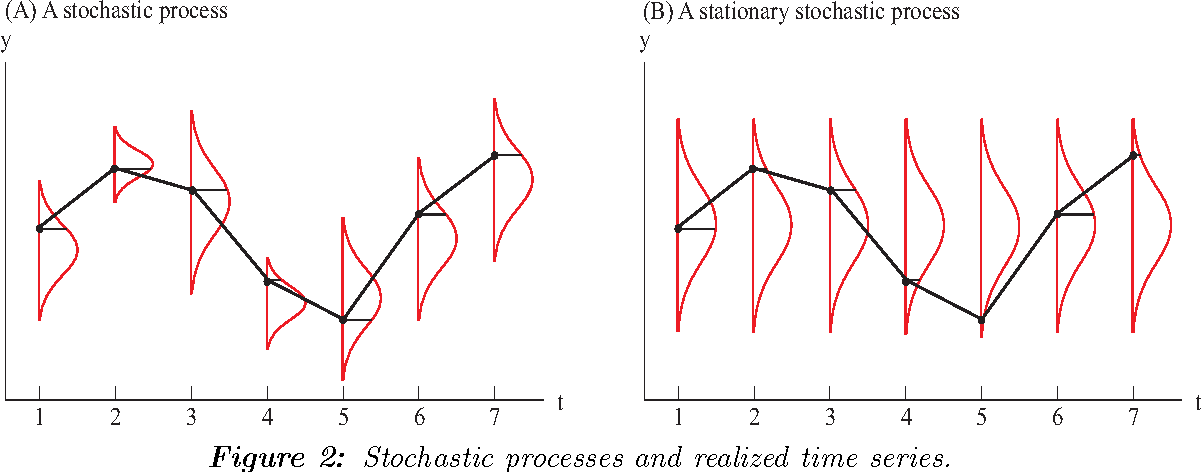
A stochastic process is said to be stationary in the strict sense if all the random variables that make up the process are identically distributed, regardless of the moment in time at which the process is studied.

That is, the probability distribution function of any set of \(k\) variables (\(k\) being a finite number) of the process must remain stable (unchanging) as the variables are shifted \(s\) periods of time such that, if \(P(Y_{t+1}, Y_{t+2}, ..., Y_{t+k} )\) is the cumulative probability distribution function, then:

\[ P(Y_{t+1},Y_{t+2},…,Y_{t+k}) = P(Y_{t+1+s}, Y_{t+2+s},…,Y_{t+k+s}),\ \ \forall t, k, s \]

However, the strict version of the stationarity of a process is usually too restrictive. For this reason, weak or second-order stationarity is generally used, which occurs when the mean of the process is constant and independent of time, the variance is finite and constant, and the value of the covariance between two periods depends only on the distance or lag between them, regardless of the moment in time at which they are calculated.

A time series is stationary (in the weak sense) when the level and covariances of the series do not change over time.

In other words, a time series is stationary when it evolves in time randomly around a constant mean, showing some form of stable equilibrium.

• In simple terms, a time series is stationary if its behavior does not change over time. This means, for example, that the values always tend to vary around the same level and that their variability is constant over time.

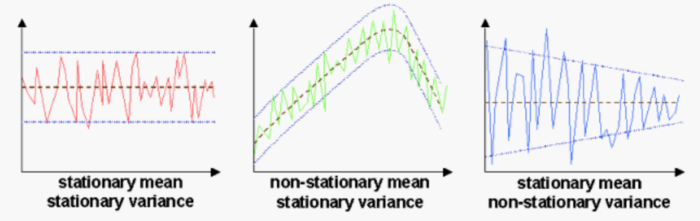
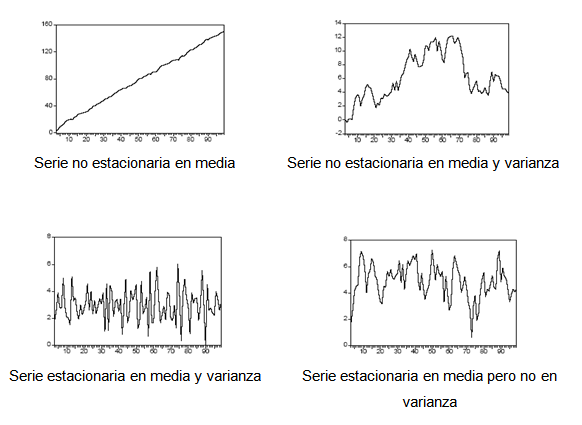
For stationary series a lot of theory is available since their behavior is well known. They therefore play a fundamental role in the study of time series.

Why is it important for the researcher that the process under analysis is stationary?

The fundamental reason is that the time series prediction models we will see below are designed to be used with processes of this type. If the characteristics of the process change over time, it will be difficult to represent the series for past and future time intervals using a simple linear model, and therefore reliable forecasts for the variable under study cannot be made.

However, as a general rule, economic series are not series coming from stationary processes, but usually have a trend, either increasing or decreasing, and non-constant variability. This limitation is not so important in practice because non-stationary series can be transformed into approximately stationary ones after applying differences to the series in one or more stages